Area of triangle

• 1. Area of a triangle when we know the base and the height

     The area of a triangle is equal to half of base times height.

     A =	1	a · h
     	2

  2. Area of a triangle when we know the lengths of all three of its sides (Heron's formula)

     A = √s(s - a)(s - b)(s - c)

  3. Area of a triangle when we know two sides and the included angle

     The area of a triangle is equal to half of a product of two sides and sine of the angle between this sides.

     A =	1	a · b · sin γ
     	2

     A =	1	a · c · sin β
     	2

     A =	1	b · c · sin α
     	2

  4. Area of a triangle when we know three sides and circumradius

     A =	a · b · с
     	4R

  5. Area of a triangle when we know semiperimeter and in-radius

     The area of a triangle is equal to semiperimeter times in-radius.
     

     A = s · r

     
     where A - the area of a triangle,
     a, b, c - the length of sides BC,AC,AB accordingly,
     h - the height, the length of the altitude,
     α, β, γ - the angles,
     r - the length of the in-radius,
     R - the length of the circumradius,
     

     s =	a + b + c	- the semiperimeter, or half of the triangle's perimeter.
     	2

     REFERENCE FROM onlinemschool.com/math/formula/area/

Types of quadrilateral

Congruence of Triangles

Congruence of Triangles

If two geometrical figures are identical in shape and size then they are said to be congruent.

The Method of Superposition.

Step 1 : Take a trace copy of the Fig. 1. We can use Carbon sheet.

Step 2 : Place the trace copy on Fig. 2 without bending, twisting and stretching.

Step 3 : Clearly the figure covers each other completely.

Therefore the two figures are congruent.

Congruence of Triangles

Two triangles are said to be congruent, if the three sides and the three angles of one triangle are respectively equal to the three sides and three angles of the other.

Conditions for Triangles to be Congruent

We know that, if two triangles are congruent, then six pairs of their corresponding parts (Three pairs of sides, three pairs of angles) are equal.

But to ensure that two triangles are congruent in some cases, it is sufficient to

verify that only three pairs of their corresponding parts are equal, which are given as axioms.

There are four such basic axioms with different combinations of the three pairs of corresponding parts. These axioms help us to identify the congruent triangles.

If ‘S’ denotes the sides, ‘A’ denotes the angles, ‘R’ denotes the right angle and ‘H’ denotes the hypotenuse of a triangle then the axioms are as follows:

(i) SSS axiom          (ii) SAS axiom          (iii) ASA axiom        (iv) RHS axiom

(i) SSS Axiom (Side-Side-Side axiom)

If three sides of a triangle are respectively equal to the three sides of another triangle then the two triangles are congruent.

(ii) SAS Axiom  (Side-Angle-Side Axiom)

If any two sides and the included angle of a triangle are respectively equal to any two sides and the included angle of another triangle then the two triangles are congruent.

 (iii) ASA Axiom (Angle-Side-Angle Axiom)

If two angles and a side of one triangle are respectively equal to two angles and the corresponding side of another triangle then the two triangles are congruent.

(iv) RHS Axiom (Right angle - Hypotenuse - Side)

If the hypotenuse and one side of the right angled triangle are respectively equal to the hypotenuse and a side of another right angled triangle, then the two triangles are congruent.

Multiplication-Napier bones method

Multiplying a two-digit number with another two-digit number would require a 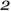 by 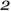 grid, for example .

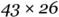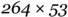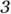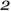Multiplying  would require a  by grid.

Follow the steps below to see how Napier’s method is used to calculate .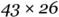

• The first step is to draw a  by  grid.
• The second step is to draw a diagonal in each box. The diagonal line separates the tens and the units. Always write the tens above the diagonal line in each box.
• Start by multiplying  and  to fill the left box on the top row.
• 
• Write  and  to show that there are no tens.

• Now multiply  and  to fill the right box on the top row.
• 

• Next, multiply  and  to fill the left box on the bottom row.
• 
• Remember to put the  above the diagonal.

• Complete the grid by multiplying  and  to fill the right box on the bottom row.
• 

After completing the grid, add the columns along the diagonals, starting at the bottom-right. We sometimes need to carry over from one diagonal to the next. To get the answer, read the totals down the left and to the right.

REFERENCE FROM https://www.bbc.co.uk/education/guides/zvvg87h/revision/2

Q

Rectangle

A rectangle is a shape with four sides and four corners. The corners are all right angles. It follows that the lengths of the pairs of sides opposite each other must be equal.

People make many rectangular things, including most tables, boxes, books, and papers.

A rectangle with all four sides equal in length is called a square.

PROPERTIES OF RECTANGLE:

1. The opposite sides are equal.
2. All angles are equal.
3. Each angle is a right angle.
4. The diagonals are equal in length.
5. The diagonals bisect each other.

FORMULAS OF RECTANGLE:

 Area of Rectangle=length*breadth

                              =l*b sq.units.

Perimeter of Rectangle=2(l+b) units.

Square

A square is a shape with four equal sides and four corners that are all right angles (90 degrees). The diagonals of a square also cross at right angles. The angle between any diagonal and a side of a square is 45 degrees. A square has rotational symmetry of four. It has four lines of regular symmetry.

A square is a type of rectangle with all sides of equal length. However note that while a square is a type of rectangle, a rectangle does not necessarily need to be a square.

A square is also the 2-dimensional analogue of a cube.

PROPERTIES OF SQUARE:

1. All the angles are equal.                                                                    
2. All the sides are of equal length.
3. Each of the angle is a right angle.
4. The diagonal are of equal length and breadth.
5. The diagonals bisect each other at right angles.

FORMULAS:

  Area of square=side*side

                       A=a*a 

                         =a² sq.units

 Perimeter of square=4a units

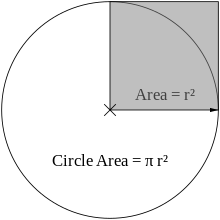
Circle

A circle is a round, two-dimensional shape. All points on the edge of the circle are at the same distance from the centre.

The radius of a circle is a line from the centre of the circle to a point on the side. Mathematicians use the letter r for the length of a circle's radius. The centre of a circle is the point in the very middle.

The diameter (meaning "all the way across") of a circle is a straight line that goes from one side to the opposite and right through the centre of the circle. Mathematicians use the letter d for the length of this line. The diameter of a circle is equal to twice its radius (d equals 2 times r).

${\displaystyle d=2\ r}$

The circumference (meaning "all the way around") of a circle is the line that goes around the centre of the circle. Mathematicians use the letter C for the length of this line.

The number π (written as the Greek letter pi) is a very useful number. It is the length of the circumference divided by the length of the diameter (π equals C divided by d). As a fraction the number π is equal to about ²²⁄₇ or 335/113 (which is closer) and as a number it is about 3.1415926535.

	${\displaystyle \pi ={\frac {C}{d}}}$
${\displaystyle \therefore }$	${\displaystyle C=2\pi \,r}$

The area, a, inside a circle is equal to the radius multiplied by itself, then multiplied by π (a equals π times r times r).

${\displaystyle A=\pi \,r^{2}}$

Calculating π

π can be measured by drawing a large circle, then measuring its diameter (d) and circumference (C). This is because the circumference of a circle is always π times its diameter.

${\displaystyle \pi ={\frac {C}{d}}}$

π can also be calculated by only using mathematical methods. Most methods used for calculating the value of π have desirable mathematical properties. However, they are hard to understand without knowing trigonometry and calculus. However, some methods are quite simple, such as this form of the Gregory-Leibniz series:

${\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots }$

While that series is easy to write and calculate, it is not easy to see why it equals π. An easier to understand approach is to draw an imaginary circle of radius r centered at the origin. Then any point (x,y) whose distance d from the origin is less than r, calculated by the pythagorean theorem, will be inside the circle:

${\displaystyle d={\sqrt {x^{2}+y^{2}}}}$

Finding a set of points inside the circle allows the circle's area A to be estimated. For example, by using integer coordinates for a big r. Since the area A of a circle is π times the radius squared, π can be approximated by using:

${\displaystyle \pi ={\frac {A}{r^{2}}}}$

REFERENCE FROM WIKIPEDIA