Amazing facts about Numbers

• India invented the Number System. Zero was invented by Aryabhatta. The place value system, the decimal system was developed in India in 100 BC.
• The largest numbers the Greeks and the Romans used were 10^6 whereas Hindus used numbers as big as 10^53 with specific names as early as 5000 BC during the Vedic period. Even today, the largest used number is Tera: 10^12.
• It took a Hitachi SR 8000 supercomputer over 400 hours to compute pi to 1.24 trillion digits where pi can’t be expressed as a fraction and never ends and repeats when written as a decimal (The ratio of the circumference to the diameter of a circle :- 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510…..).
• 2 and 5 are the only prime numbers that end with a 2 or a 5.
• Zero is the only number known with so many names which include zip, zilch, nil, nought, naught.
• Googol is the number “one” followed by one hundred zeros. Infact Google’s name came from misspelling of this word.
• The opposite sides of a dice always add up to seven. From number 0 to 1000, the letter ‘A’ only appears in 1000 (One thousand).

Basic Definitions of Numbers

ALGEBRAIC NUMBERS: Algebraic numbers are the real or complex number solutions to polynomial equations of the form:

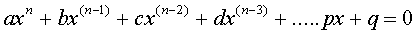
The coefficients a, b, c, d, ....p, q, are integers or fractions. All rational numbers are algebraic while some irrational numbers are algebraic.

ALIQUOT PART: An aliquot part is any divisor of a number, not equal to the number itself. The divisors are often referred to as proper divisors. The aliquot parts of the number 24 are 1, 2, 3,4, 6, 8 and 12..

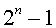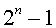ALMOST PERFECT NUMBER: An almost perfect number is typically applied to the powers of 2 since the sum of the aliquot parts is or just 1 short of being a perfect number. It follows that any power of 2 is a deficient number

ALPHAMETIC NUMBERS:  Alphametic numbers form cryptarithms where a set of numbers are assigned to letters that usually spell out some meaningful thought. The numbers can form an addition, subtraction, multiplication or division problem. One of the first cryptarithms came into being in 1924 in the form of an addition problem the words being intended to represent a student's letter from college to the parents. The puzzle read SEND + MORE = MONEY. The answer was 9567 += 1085 = 10,652. Of course, you have to use logic to derive the numbers represented by each letter..

Basic Definitions of Numbers

Numbers - The Basics

Integers - Any of the positive and negative whole numbers, ..., -3, -2, -1, 0, +1, +2, +3, ... The positive integers, 1, 2, 3..., are called the natural numbers or counting numbers. The set of all integers is usually denoted by Z or Z+

Digits - the 10 symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, used to create numbers in the base 10 decimal number system.

Numerals - the symbols used to denote the natural numbers. The Arabic numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are those used in the Hindu-Arabic number system to define numbers.

Natural Numbers - the set of numbers, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,....., that we see and use every day. The natural numbers are often referred to as the counting numbers and the positive integers.

Whole Numbers - the natural numbers plus the zero.

Rational Numbers - any number that is either an integer "a" or is expressible as the ratio of two integers, a/b. The numerator, "a", may be any whole number, and the denominator, "b", may be any positive whole number greater than zero. If the denominator happens to be unity, b = 1, the ratio is an integer. If "b" is other than 1, a/b is a fraction.

Fractional Numbers - any number expressible by the quotient of two numbers as in a/b, "b" greater than 1, where "a" is called the numerator and "b" is called the denominator. If "a" is smaller than "b" it is a proper fraction. If "a" is greater than "b" it is an improper fraction which can be broken up into an integer and a proper fraction.

Irrational Numbers - any number that cannot be expressed by an integer or the ratio of two integers. Irrational numbers are expressible only as decimal fractions where the digits continue forever with no repeating pattern. Some examples of irrational numbers are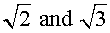 

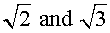
Transcendental Numbers - any number that cannot be the root of a polynomial equation with rational coefficients. They are a subset of irrational numbers examples of which are Pi = 3.14159... and e = 2.7182818..., the base of the natural logarithms.

Real Numbers - the set of real numbers including all the rational and irrational numbers.

Euclidean Geometry

 Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions (theorems) from these. Although many of Euclid's results had been stated by earlier mathematicians, Euclid was the first to show how these propositions could fit into a comprehensive deductive and logical system. The Elements begins with plane geometry, still taught in secondary school as the first axiomatic system and the first examples of formal proof. It goes on to the solid geometry of three dimensions. Much of the Elements states results of what are now called algebra and number theory, explained in geometrical language.

For more than two thousand years, the adjective "Euclidean" was unnecessary because no other sort of geometry had been conceived. Euclid's axioms seemed so intuitively obvious (with the possible exception of the parallel postulate) that any theorem proved from them was deemed true in an absolute, often metaphysical, sense. Today, however, many other self-consistent non-Euclidean geometries are known, the first ones having been discovered in the early 19th century. An implication of Albert Einstein's theory of general relativity is that physical space itself is not Euclidean, and Euclidean space is a good approximation for it only where the gravitational field is weak.

Euclidean geometry is an example of synthetic geometry, in that it proceeds logically from axioms to propositions without the use of coordinates. This is in contrast to analytic geometry, which uses coordinates.

ELEMENTS:

 MAIN ELEMENTS:EUCLID'S ELEMENTS

 The Elements is mainly a systematization of earlier knowledge of geometry. Its improvement over earlier treatments was rapidly recognized, with the result that there was little interest in preserving the earlier ones, and they are now nearly all lost.

There are 13 total books in the Elements:

Books I–IV and VI discuss plane geometry. Many results about plane figures are proved, for example "In any triangle two angles taken together in any manner are less than two right angles." (Book 1 proposition 17 ) and the Pythagorean theorem "In right angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle." (Book I, proposition 47)

Books V and VII–X deal with number theory, with numbers treated geometrically via their representation as line segments with various lengths. Notions such as prime numbers and rational and irrational numbers are introduced. The infinitude of prime numbers is proved.

Books XI–XIII concern solid geometry. A typical result is the 1:3 ratio between the volume of a cone and a cylinder with the same height and base.

REFERENCE FROM WIKIPEDIA