Basic Definitions of Numbers

Numbers - The Basics

Integers - Any of the positive and negative whole numbers, ..., -3, -2, -1, 0, +1, +2, +3, ... The positive integers, 1, 2, 3..., are called the natural numbers or counting numbers. The set of all integers is usually denoted by Z or Z+

Digits - the 10 symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9, used to create numbers in the base 10 decimal number system.

Numerals - the symbols used to denote the natural numbers. The Arabic numerals 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 are those used in the Hindu-Arabic number system to define numbers.

Natural Numbers - the set of numbers, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,....., that we see and use every day. The natural numbers are often referred to as the counting numbers and the positive integers.

Whole Numbers - the natural numbers plus the zero.

Rational Numbers - any number that is either an integer "a" or is expressible as the ratio of two integers, a/b. The numerator, "a", may be any whole number, and the denominator, "b", may be any positive whole number greater than zero. If the denominator happens to be unity, b = 1, the ratio is an integer. If "b" is other than 1, a/b is a fraction.

Fractional Numbers - any number expressible by the quotient of two numbers as in a/b, "b" greater than 1, where "a" is called the numerator and "b" is called the denominator. If "a" is smaller than "b" it is a proper fraction. If "a" is greater than "b" it is an improper fraction which can be broken up into an integer and a proper fraction.

Irrational Numbers - any number that cannot be expressed by an integer or the ratio of two integers. Irrational numbers are expressible only as decimal fractions where the digits continue forever with no repeating pattern. Some examples of irrational numbers are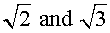 

Transcendental Numbers - any number that cannot be the root of a polynomial equation with rational coefficients. They are a subset of irrational numbers examples of which are Pi = 3.14159... and e = 2.7182818..., the base of the natural logarithms.

Real Numbers - the set of real numbers including all the rational and irrational numbers.